This post will cover parts 18-26 of Section 3, Module 1, Unit 1.
Circular Motion
Simply enough, circular motion is just motion in a circle. However, when you think about the implications of that, you'll realize that everything we know about motion must now happen in a circular pattern- displacement must now happen at an angle (angular displacement), velocity must now occur at an angle (angular velocity) and there has to be some form of force that keeps pulling the object in circular motion towards the center of the circular path (centripetal force).
We'll be discussing uniform circular motion, that is, motion in a circle at a constant speed. You'll realize that although speed is constant, velocity is not constant since it changes based on direction.
Let's take a start by looking at circular motion on a diagram:
As you can see, the motion of that green object is occurring in the direction of velocity, which is acting at a tangent (line perpendicular to the radius) to the circle. If the starting point was at the x-axis, the displacement of the object is that curved line labelled s. This is called the angular displacement, s. The angle at which this displacement has occurred there is labelled as θ, and, if we show the object's location at other points along the path:
You'll see that r, the radius of the circle, remains constant, and the angular displacement seems to be directly related to the angle θ. If you did CSEC Add Math, you'll know that they are, and s is essentially the arc length:
Of course, this can be rearranged to find whichever of the values you need. You should be aware, however, that this angle is not in degrees, but rather in radians.
You can remember that first equation and rearrange it based on whatever conversions you need to do.
The angular velocity (ω, common omega) is distinct from the velocity of the object in circular motion. While the velocity of the object is always changing direction (but has the same magnitude), the angular velocity is a constant value. The angular velocity is the change in the size of the angle per second. This is shown as:
The SI Units of angular velocity are therefore radians per second. Sometimes, you will get values in revolutions per second or revolutions per minute. One revolution is a movement through an angle of 360 degrees, or 2Ï€ radians. So, simply multiply the revolutions per second value by 2Ï€ to get the value in rad/s.
The period (T) of a particle undergoing uniform circular motion is the time taken for one complete revolution. If it goes through n revolutions in a time t, the period is found as:
Frequency is the number of revolutions per second, and is the reciprocal of the period, T:
Using this, if we want to express angular velocity for one complete revolution, θ is 2π radians and t is the same as the period T:
We mentioned earlier that speed was constant throughout uniform circular motion. We refer to speed as linear speed here, represented with the symbol v (kind of confusing, I know, but v is used for both speed and velocity in physics). Linear speed is simply the rate of change of angular displacement (s):
In order for an object to maintain a circular path, there has to be a force that keeps pulling it towards the center. This force is called centripetal force. If the centripetal force were to stop acting on the object at any point, the object would just continue along a straight line (at a tangent to the circular path) at the linear velocity. Since a force is acting towards the center of the circular path, the object is accelerating towards the center. We refer to this acceleration as centripetal acceleration.
For centripetal acceleration, we'll look at a specific proof. Let's say we had the circular motion of a particular object at two points along its path:
We can represent these two velocities at these points as a separate triangle:
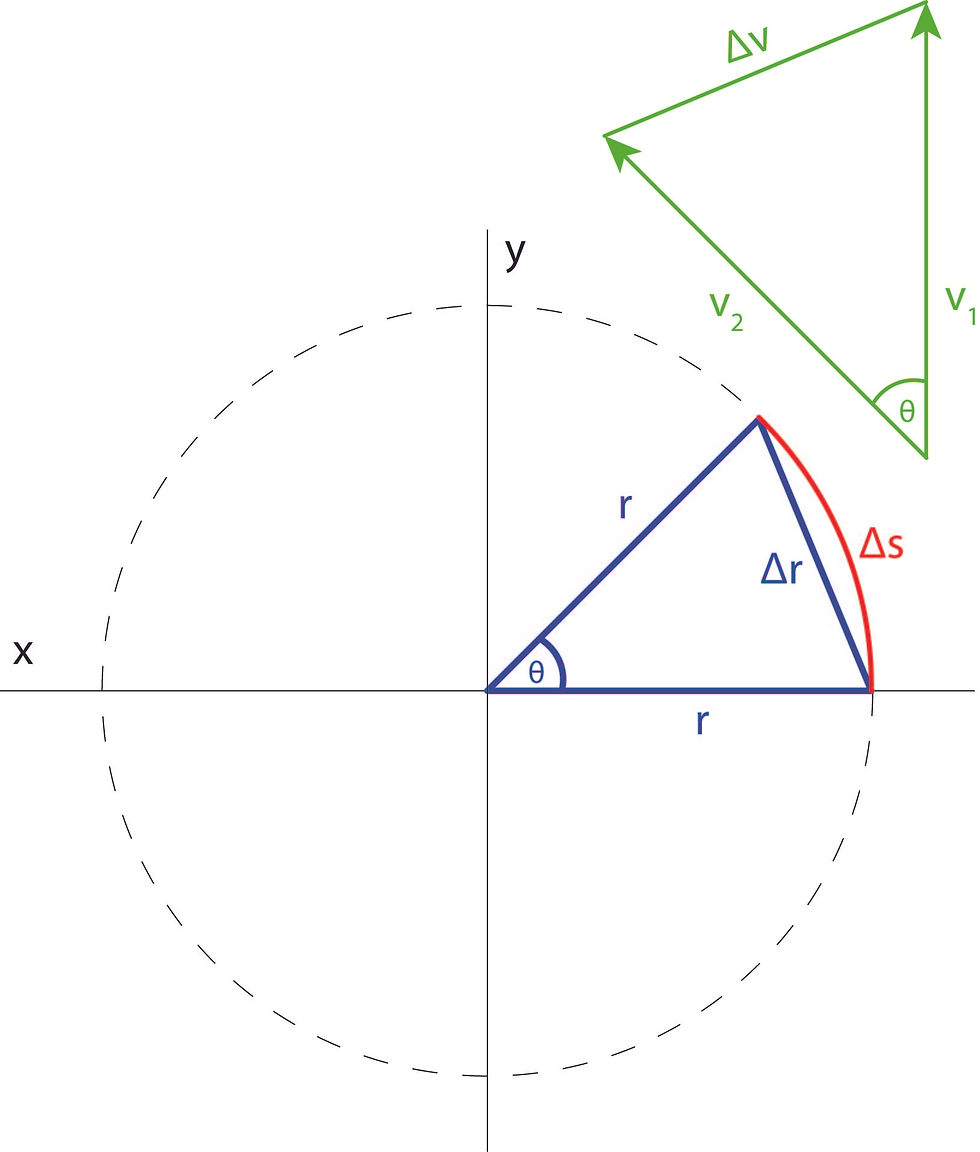
I've also highlighted the change in angular displacement, or the arc length on the diagram. The two triangles seen above are similar triangles, as the angle theta is the same for both of them and they are both isosceles triangles, since linear velocity is constant (v1 and v2 are the same) and r is constant.
At a small enough angle, the arc length (change in displacement) is basically the same as the ∆r. We can essentially equate these relationships, since the ratio of two sides in similar triangles is equal:
These two equations are used to find centripetal acceleration. Here it is again just to reiterate:
If you remember Newton's second law, F=ma, then you'll easily know how to find the centripetal force:
Gravitation
Isaac Newton (the biggest household name in classical mechanics) stated a law describing gravity, known as the law of universal gravitation:
All objects attract each other with the force of gravity. The force of attraction between two objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
This can be stated mathematically as:
Where F is the force of attraction between two objects, m1 is the mass of the first object, m2 is the mass of the second object, r is the distance between the centers of the two objects and G is the universal gravitation constant, 6.67x10^-11 Nm^2/kg^2
The gravitational field strength (g) at a point is defined as the gravitational force per unit mass at that point in the field. The gravitational force of a mass is referred to as its weight (W). You have definitely come across this equation in the past:
Which can be rearranged for g:
Showing that the unit of g is N/kg. However, we know that the force acting on an object is proportional to its acceleration in the equation F=ma, so W=ma and therefore:
The gravitational field strength is numerically equal to the acceleration due to gravity.
If we use the universal law of gravitation, we can determine the gravitational field strength acting on an object a certain distance above the surface of a body like the earth. Since W is F when we consider the earth as the subject:
Remember that r should be the distance between the centers of the two bodies in question, so the distance above the surface of the earth (h) must always be added to the earth's radius (R) unless it is explicitly stated that the distance given is the distance from the Earth's center.
Near-Earth and Medium Earth Satellites
A satellite is any object that orbits another body due to the influence of gravity. Near-Earth Satellites (in Low Earth Orbit) are used for photographing and monitoring details on the earth's surface, such as crop growth, aircrafts and weather progression. They are usually found at between 200 and 2000km above the earth's surface.
A synchronized system of satellites orbiting the earth with a period of 11 hours and 58 minutes at 20,200km above the earth forms a Global Positioning System (GPS). A receiver can interface with three of these satellites to determine its current latitude, longitude and movement.
The satellite therefore travels a circular path. This means that we can go ahead and use some of the circular motion equations we saw earlier.
The force of attraction due to gravity, F or W, is basically the centripetal force of a satellite in orbit.
Starting with the relationship above, you can substitute to get whatever other value you want!
But how about finding the velocity of a satellite?
What if we wanted to fine the period of a satellite (i.e. how long it would take to complete one orbit)?
Geostationary Satellites
Geostationary satellites are kind of like 'fixed satellites,' as they are always at the same relative position over the earth's surface. A geostationary satellite has the same orbital period as the rotational period of the earth about its axis (~24 hours), so the earth moves through the same angle as the satellite in the same time.
Geostationary orbits are always above the equator. The height of a geostationary orbit is about 36000km above the surface of the earth.
Geostationary satellites are used to track weather phenomena, tectonic plate movements and global telecommunications. It makes sense that telecommunications satellites are 'parked' so that they can always provide coverage to the same area.
Comments