CSEC Physics: Motion in a Straight Line
- JH@Quelpr

- May 17, 2020
- 2 min read
Before we discuss the dynamics of motion, there are a few terms that you must understand:
Distance, s (a scalar quantity) is the total length of space between two points.
Displacement, s (a vector quantity) is the distance moved in a specific direction, or an object's overall change in position.

Speed, v (a scalar quantity) is the distance moved per unit time.
Velocity, v (a vector quantity) is the rate at which an object moves in a certain direction, or the displacement per unit time.
v= s/t
Acceleration, a (a vector quantity) is rate at which velocity changes, or the change in velocity per unit time.
a= (v-u)/t
where v = final velocity;
u = initial velocity
t = time taken
Motion Graphs
We can plot a graph that describes the motion of an object:
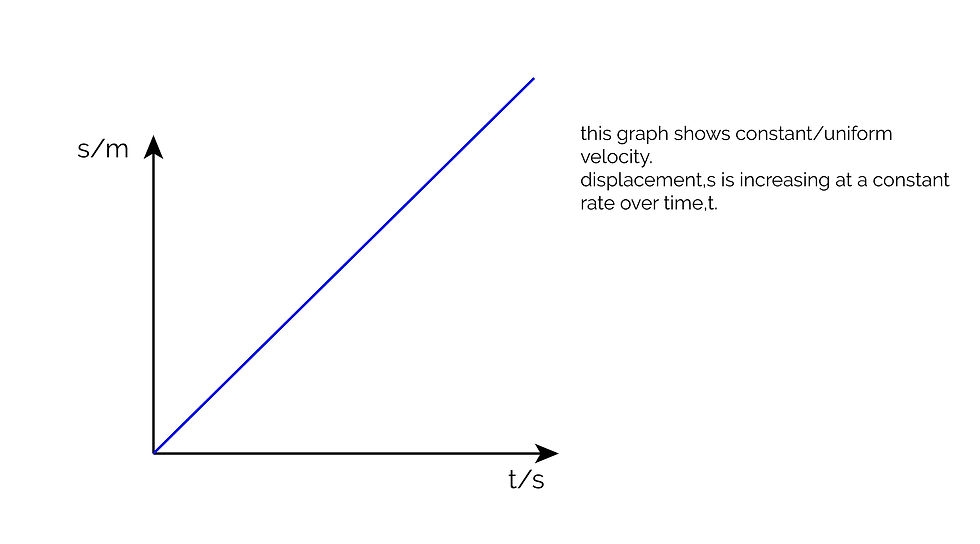
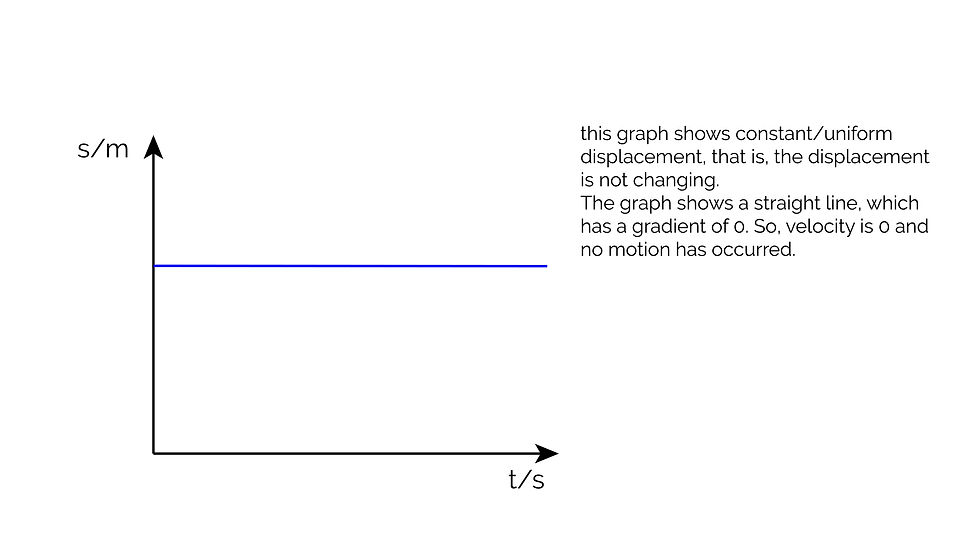
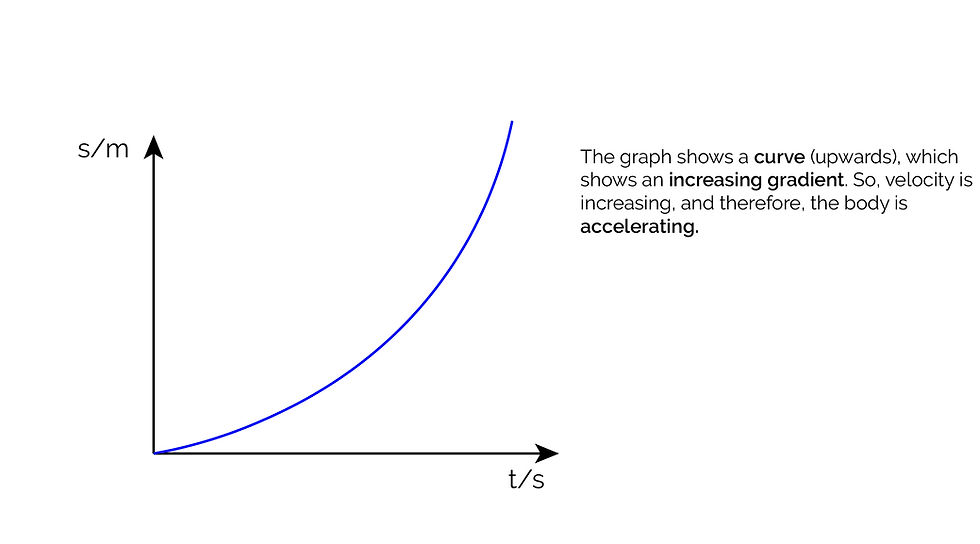
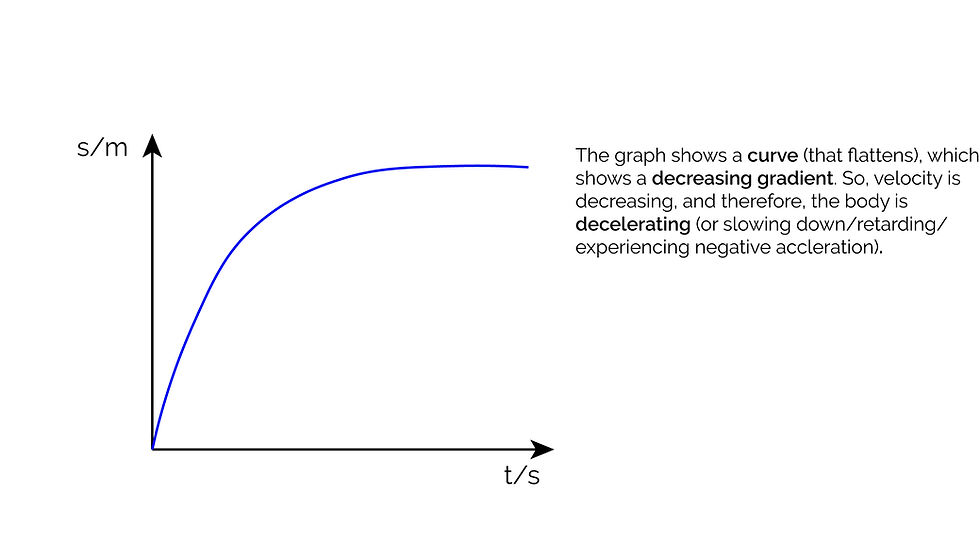
Displacement-Time Graphs
These graphs have displacement on the y axis and time on the x axis. Hence, the gradient of a displacement-time graph gives the velocity of the object.
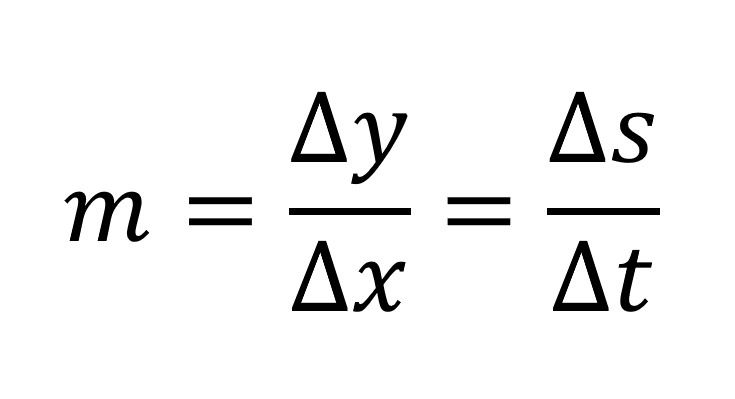
Graph 1:
Graph 2
Graph 3
Graph 4
Velocity-Time Graphs
These graphs have velocity on the y axis and time on the x axis. Hence, the gradient of a velocity-time graph gives the acceleration of the object.
Therefore the gradient, m:

Graph 1
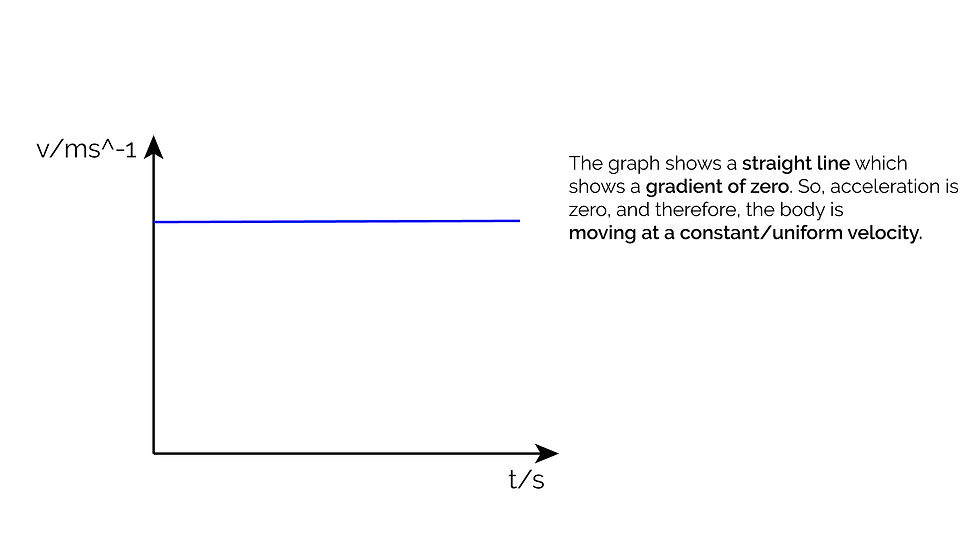
Graph 2
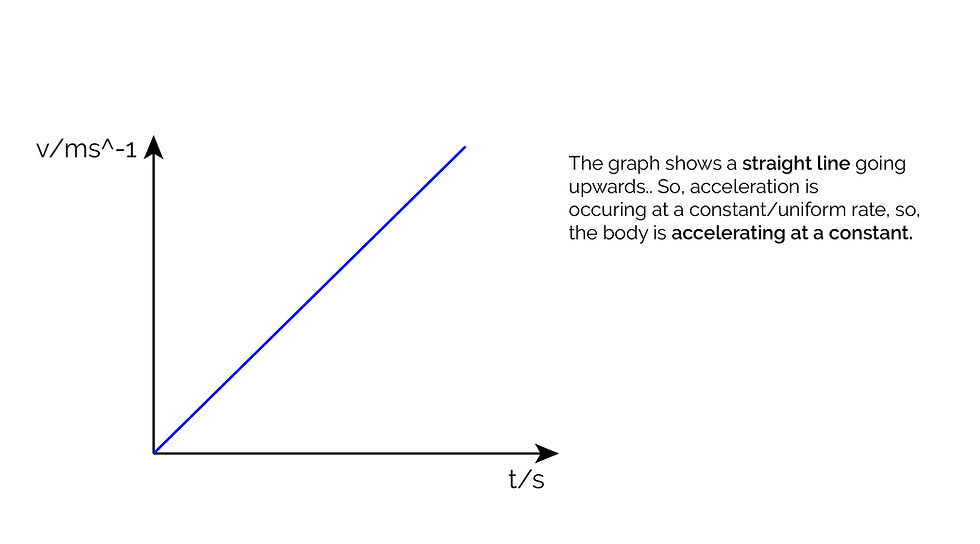
Graph 3
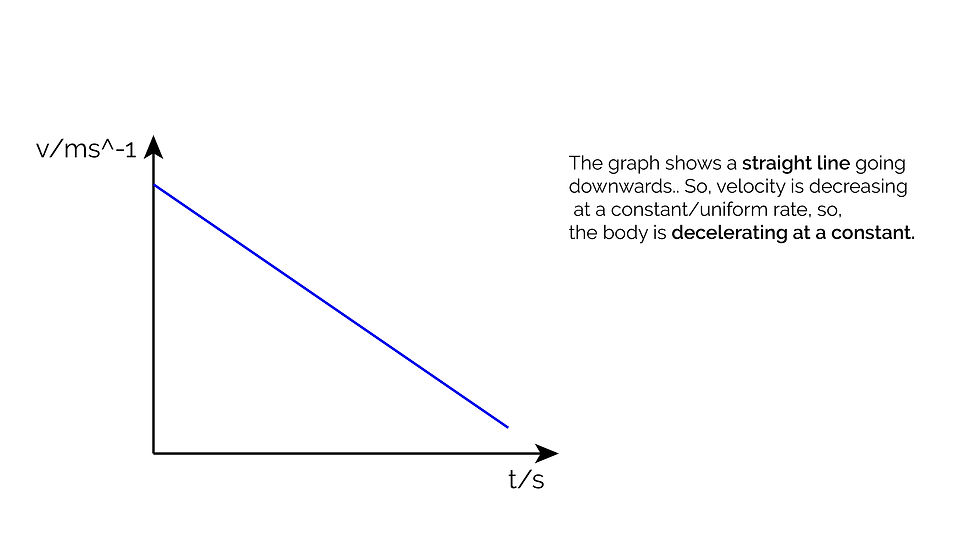
Graph 4
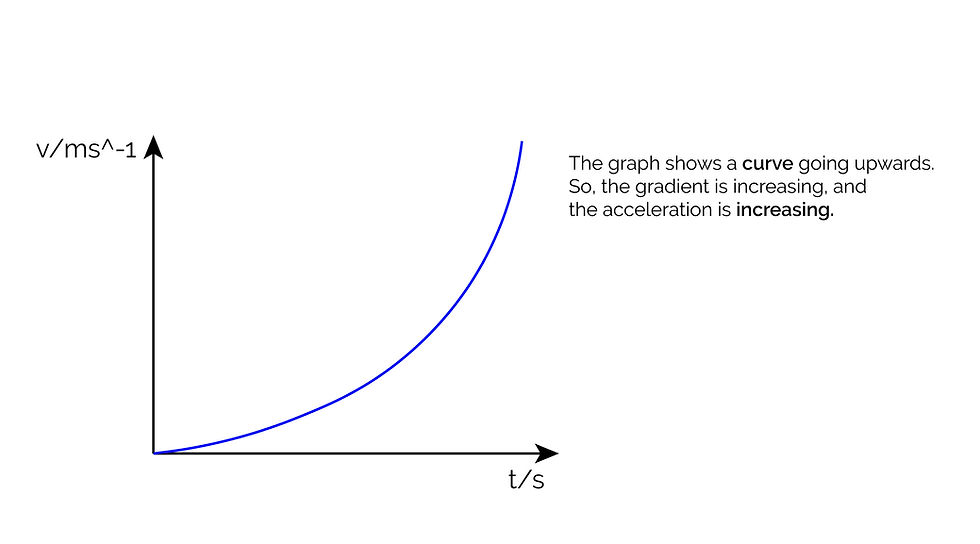
Graph 5
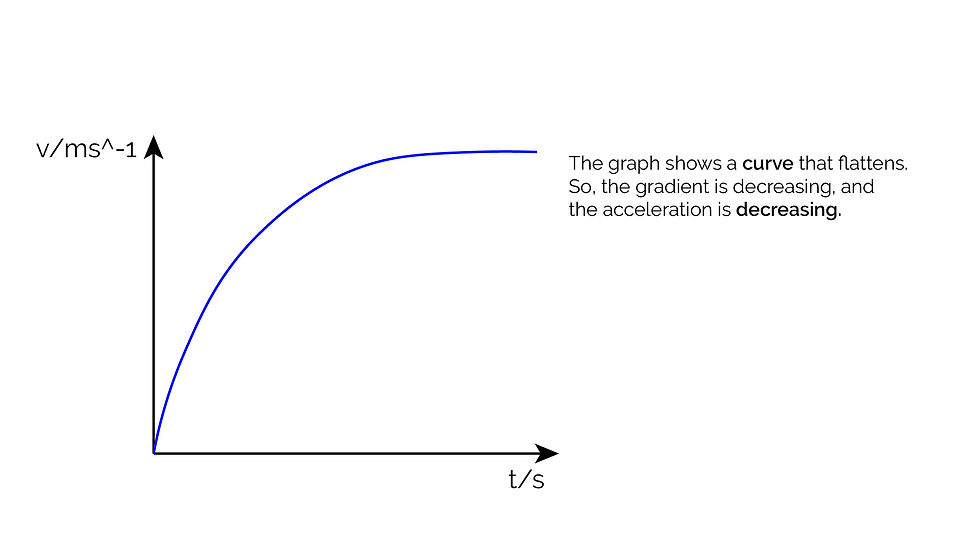
Knowing all of this, you should be able to describe and object's motion based on its motion graph or vice versa:
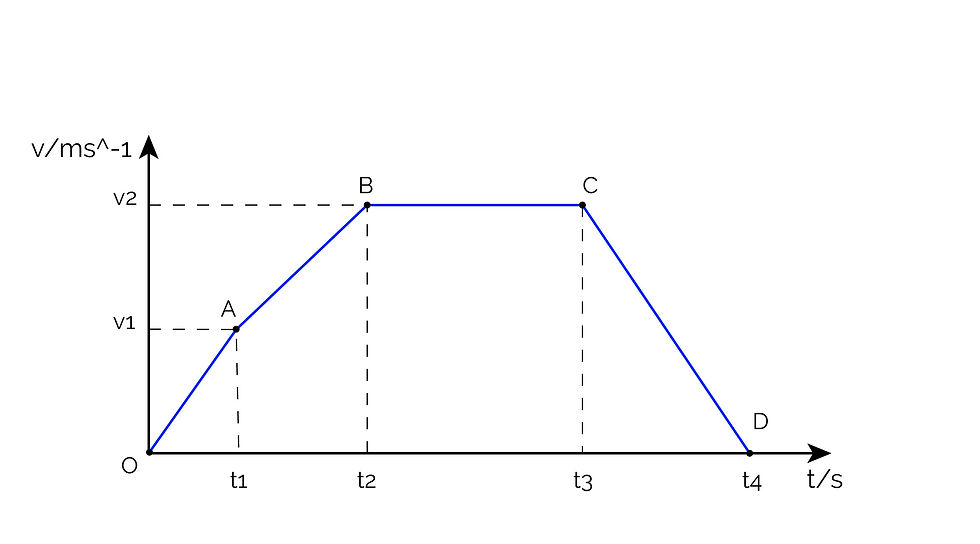
If the graph above describes the motion of a truck, then:
OA- the truck is accelerating uniformly from rest for t1 seconds until it reaches a velocity of v1.
AB- the truck's acceleration decreases slightly in t2-t1 seconds from v1 to v2.
BC- the truck moves with a constant/uniform velocity of v2 for t3-t2 seconds. The truck does not accelerate.
CD- the truck decelerates uniformly from v2 to rest in t4-t3 seconds.





Comments