CSEC Physics: Gas Laws and the Kelvin Scale
- JH@Quelpr

- Apr 27, 2020
- 4 min read
In this lesson, we will dicuss:
relating graphs of pressure or volume against temperature to the establishment of the Kelvin temperature scale;
the relationship between the Kelvin and Celsius scale;
the gas laws;
qualitative explanations of the gas laws in terms of the Kinetic theory.
To begin considering the Kelvin scale, we must first establish why it was created. Say for example, we conduct an experiment to investigate the relationship between pressure and temperature of a gas using a container filled with a certain mass of gas. The temperature and pressure of the gas are recorded. During the experiment:
temperature is varied in 10 degrees Celsius steps between 0 degrees Celsius and 100 degrees Celsius and;
the volume of gas is kept constant.
The results from the experiment give this when plotted on a graph:
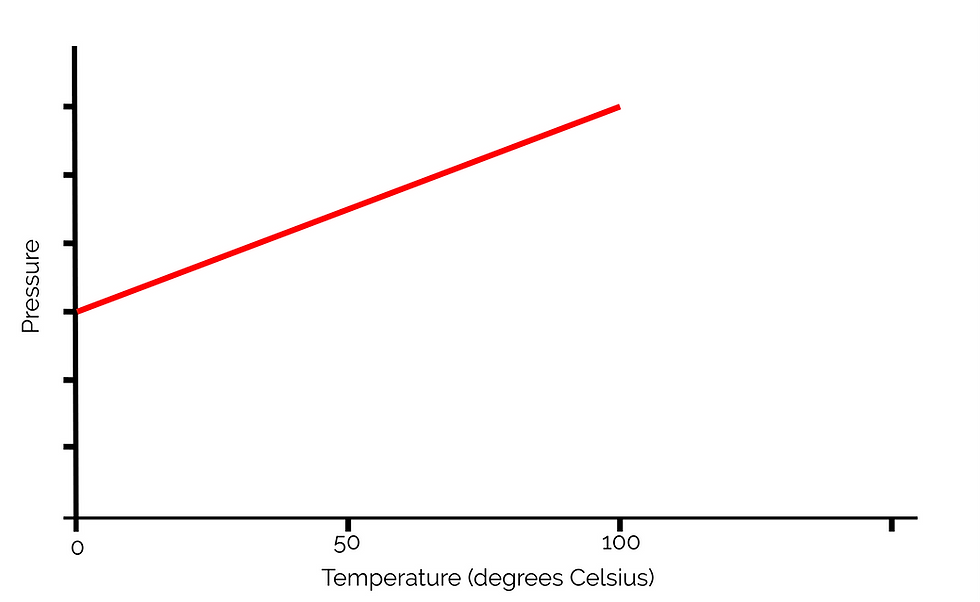
This graph tells us that as temperature increases, kinetic energy increases and so, the pressure increases as well. However, if we extrapolate this graph to find the x-intercept:
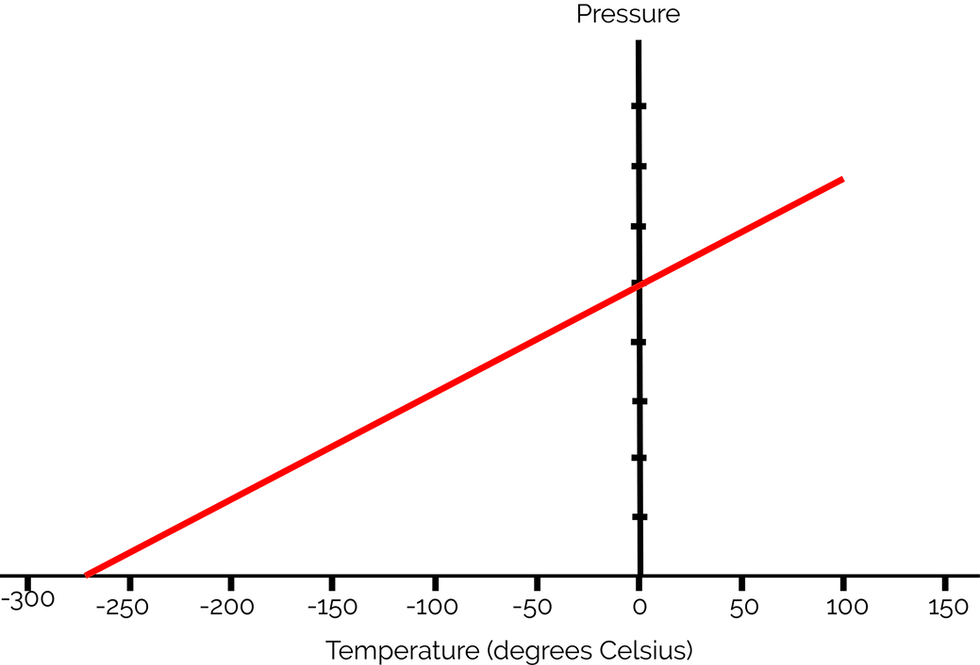
As you can see, the pressure is 0 when the temperature is -273 degrees Celsius. Lord Kelvin used this principle to develop the Kelvin temperature scale. This point is also where all molecular and atomic motion stops (kinetic energy is zero).
The basis of the Kelvin scale is that:
0 Kelvin = -273 degrees Celsius
0 degrees Celsius = 273 Kelvin
100 degrees Celsius = 373 Kelvin
Temperature in Kelvin = Temperature in Celsius + 273
A temperature increase of 1 degree Celsius is the same as a temperature increase of 1 Kelvin.
The main purpose of the Kelvin scale is to directly relate temperature to pressure. Since they are related, if you double the temperature in Kelvin, you double the pressure.
In the experiment posited, a mass of gas is heated in a container of fixed volume. When the gas is heated the particles gain kinetic energy which makes them move faster. This means they collide with the walls more frequently and with greater force and so the pressure increases.
If we change the units of the graph to Kelvin, we can see that temperature in Kelvin is directly proportional to pressure:
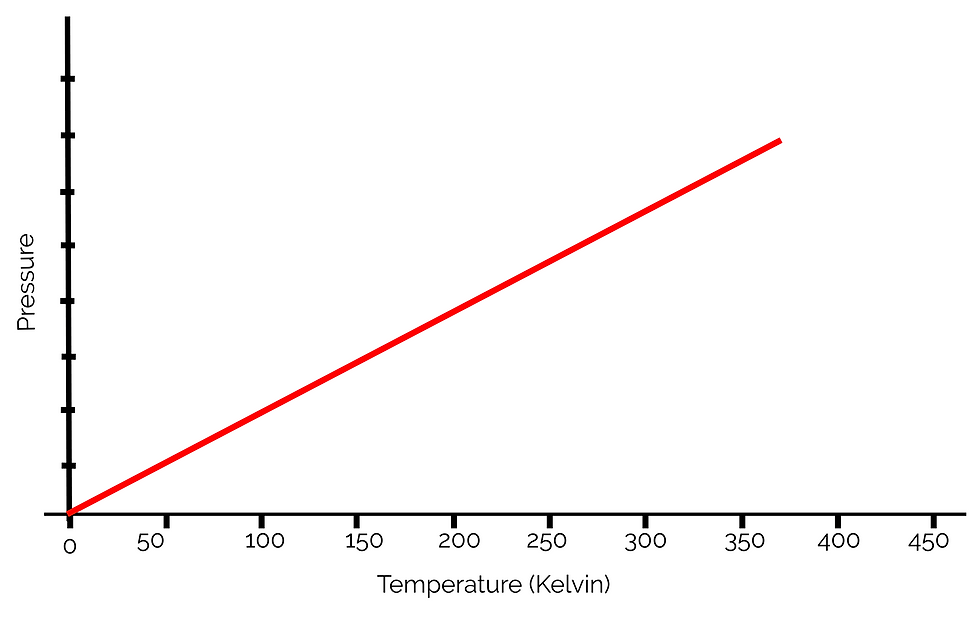
Now that we know the relationship between the Kelvin scale and the pressure of gases, we can begin discussing the gas laws.
In the 17th and 18th centuries, the gas laws were created in order to help scientists determine the pressures, volumes and temperatures of gases. The physical properties of any gas can be described completely (more or less) by four variables:
pressure (P)
volume (V)
temperature (T)
amount (n, number of moles)
The gas laws consist of four primary laws:
Charles' Law (The Temperature-Volume Law)
Boyle's Law (The Pressure-Volume Law)
Avogadro's Law (The Volume Amount Law)
Gay-Lussac's Law (The Pressure Temperature Law)
These four laws combine to form the ideal gas law and the general gas equation.
We will now cover each of the laws in detail. Before we start, however, you should know that if a certain variable is not given in the law, you should assume that the gas is under a set of standard conditions:
Temperature is Absolute Zero (Kelvin): 0 K
Pressure: 1 Atmosphere (760 mmHg)
Amount: 1 mol = 22.4 liters of gas
Charles' Law (The Temperature-Volume Law)
In 1787, French physicist Jacques Charles, discovered that the volume of a given amount of gas held at constant pressure is directly proportional to the Kelvin temperature.
V∝T
V= constant x T
The constant depends on amount of gas and pressure. So, as volume goes up, so does temperature, and vice versa.
This equation can also be described as saying that the volume divided by the temperature of a gas is constant:
V/T = constant
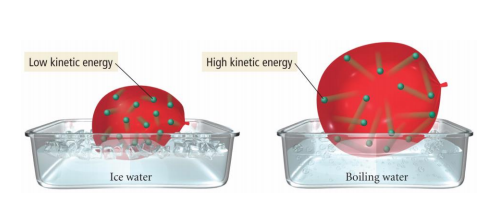
As the balloon warms up, the gas particles start to move faster, and hit the walls of the balloon harder and more frequently. For the pressure to remain constant, the balloon must expand, so the collisions occur over a larger area.
Boyle's Law (The Pressure-Volume Law)
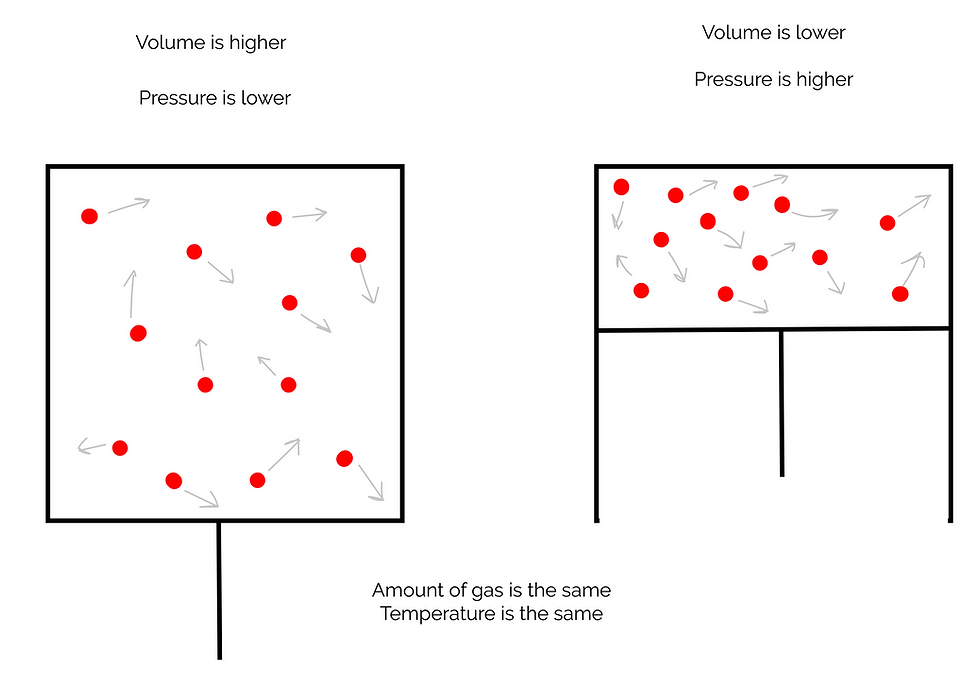
In 1662, Robert Boyle discovered that the volume of a given amount of gas held at constant temperature is inversely proportional to the pressure when the temperature and mass are constant.
P∝1/V
As pressure increases, volume decreases. Another way of saying this is that the product of the pressure and volume of a gas are constant.
P x V = constant
As the volume of the gas decreases, the gas particles have less room to move around in, and they collide more often with the walls of the container, thus increasing the pressure:
Avogadro's Law (The Volume Amount Law)
In 1811, Amadeo Avogadro discovered that volume and amount of gas (in moles) are directly proportional when pressure and temperature are held constant.
V∝n
So, if the amount of gas is increased, volume will also increase, and vice versa.
This is the same as saying that the volume divided by the amount of gas is constant:
V/n = constant
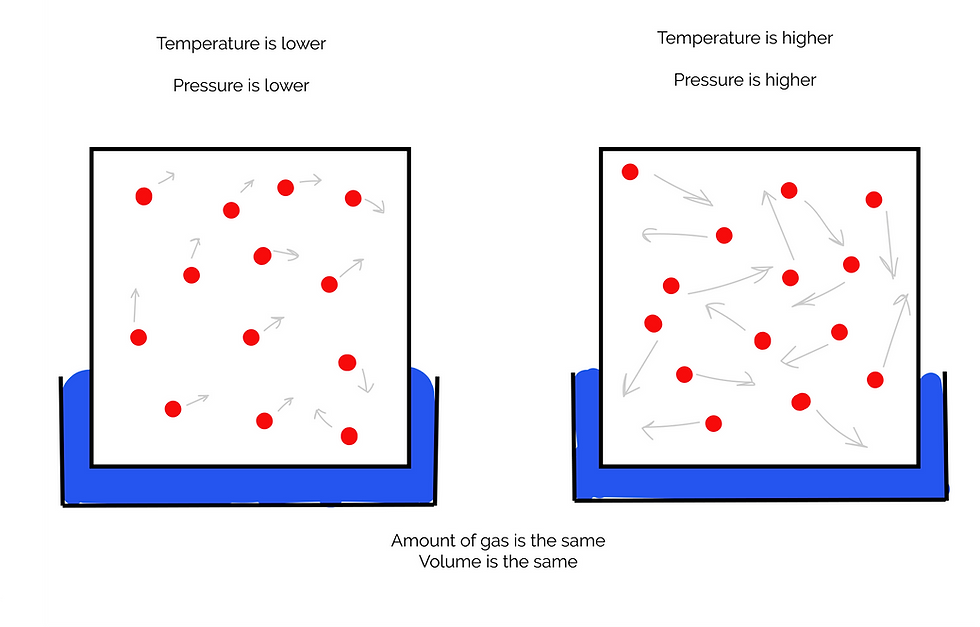
Gay-Lussac's Law (The Pressure Temperature Law)
This law states that the pressure of a given amount of gas held at constant volume is directly proportional to the Kelvin temperature.
P ∝ T
So, if pressure increases, so will the temperature, and vice versa.
This is the same as saying that the pressure of a gas divided by the temperature will be constant.
P/T = constant
General (Combined) Gas Law
All of the previous laws can be combined into a single proportion:
V ∝ T/P
The volume of a given amount of gas is proportional to the ratio of its Kelvin temperature and its pressure.
We can introduce a constant again:
PV/T= constant
(CSEC doesn't require knowledge of the ideal gas law, but you can read up on it here)
Additional Reading





Comments