CSEC Physics: Conservation of Linear Momentum

As you know, energy can neither be created nor destroyed (the law of conservation of energy). The law of conservation of linear momentum is in line with this, and states that the total momentum in an isolated (or closed) system remains constant.

A system in physics is essentially a collection of objects in whose motion you are interested. For example, if you are observing the collision of two cars, the system consists of the two cars. A system is isolated when the total mass of the system remains constant and the net external force acting on the system is zero.

So, in order for momentum to be conserved, the total mass of the system must remain the same- that is, even if mass is removed from one object, it must be added to the other object, keeping the mass constant. There should also be no net external forces acting on the system- so, the objects in the system can exert forces on each other (internal forces) but no net external force should be exerted on the objects. However, if an external force like gravity or friction acts on all objects in the system, the momentum of the entire system changes, so conservation of momentum still occurs.

We can show the conservation of momentum like this:

p₁ + p₂ = constant

or

p₁(initial) + p₂(initial) = p₁(final) + p₂(final)

As you know, p (momentum) is calculated with mass × velocity:

m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂

where:

m = mass of object

u = initial velocity

v = final velocity

For example, look at the collision between two billiard balls:

The two balls comprise a closed system. Once the cue ball is hit by the cue stick, it now has momentum because it has a velocity. It collides with the other cue ball and transfers some of its momentum to it.

Let's look in detail at this collision.

Before collision:

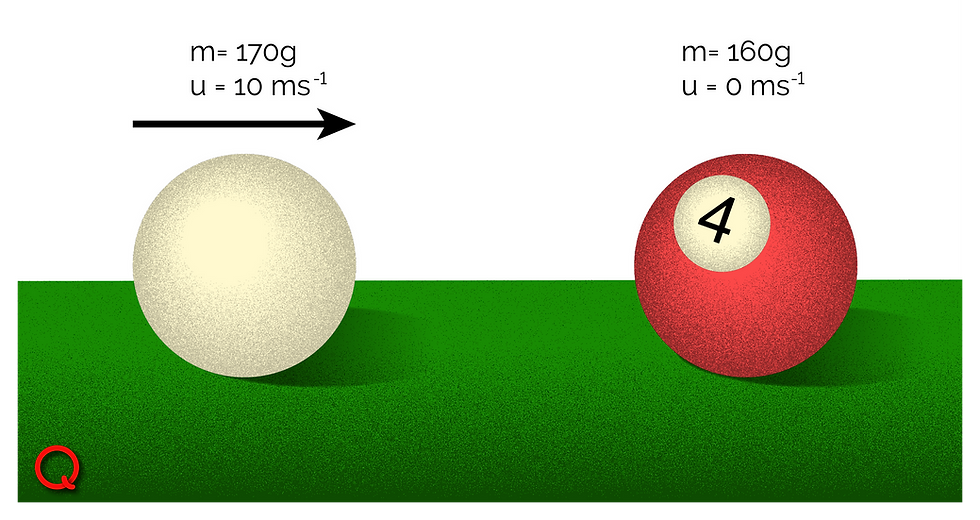
The mass of the cue ball is 170 g, and it moves at a velocity of 10 m/s. So, we can find its momentum like this:

p of cue ball = mu

= 170 g × 10 m/s

= 0.17 kg × 10 m/s

= 1.7 kgm/s

The mass of the red ball is 160 g (0.16 kg) and it is at rest:

p of red ball = mu

= 0.16 kg × 0 m/s

= 0 kgm/s

After the collision, given that the red ball travels away at 11 m/s.

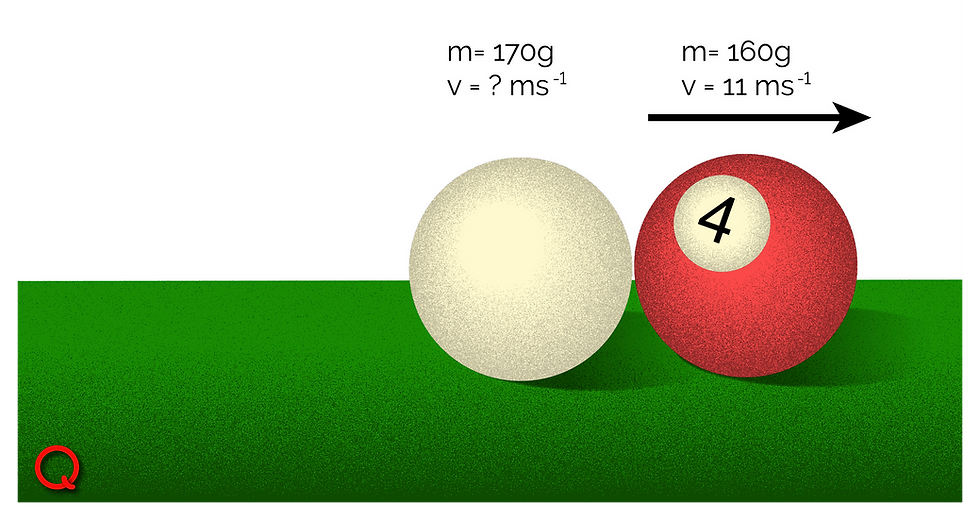
We can use the law of conservation of momentum here to determine the velocity of the cue ball after the collision:

m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂

0.17 kg × 10 m/s + 0.16 kg × 0 m/s = 0.17 kg × v₁ + 0.16 kg × 11 m/s

1.7 kgm/s + 0 kgm/s = 0.17 kg × v₁ + 1.76 kgm/s

1.7 kgm/s = 0.17 kg × v₁ + 1.76 kgm/s

1.7 kgm/s = 0.17 kg × v₁ + 1.76 kgm/s

1.7 kgm/s - 1.76 kgm/s = 0.17 kg × v₁

-0.06 kgm/s =0.17 kg × v₁

-0.06 kgm/s ÷ 0.17kg = v₁

v₁ = -0.35 m/s

Therefore, the cue ball moves in the opposite direction (to the left) at 0.35 m/s.

This is an example of an elastic collision, where the two objects split up after collision (as if they bounce off of each other).

A collision can also be inelastic, that is, the two objects collide and stick together, forming a singular body that moves as a unit.

For example: You and your friend decide to do something stupider than usual and throw a metal ball and a wad of pizza dough at each other. The wad of dough collides with and sticks to the ball in mid air. The metal ball has a mass of 2000 grams and the wad of pizza dough has a mass of 454 grams. Your friend is cooler and stronger than you, so he throws the metal ball at a velocity of 12 m/s, and you throw the wad of pizza dough at a velocity of 16 m/s. What is the velocity of the disgusting metal-dough abomination you have created after the collision?

We can start with a diagram showing this scenario, before and after the collision.

Before the collision:

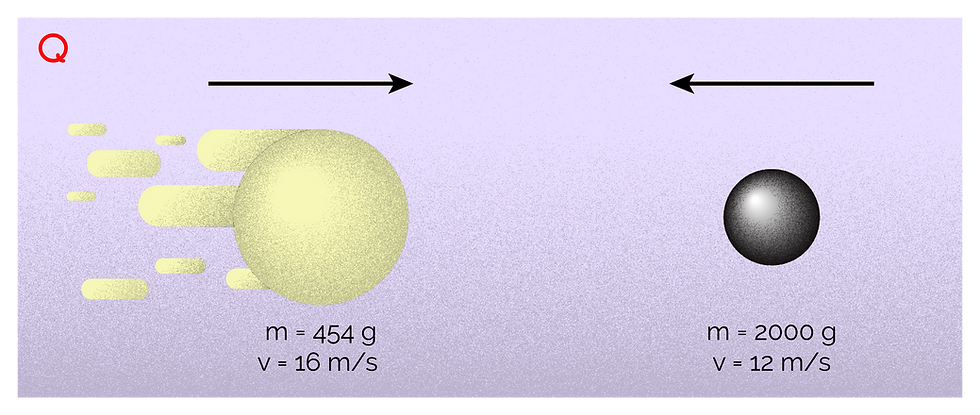
p of wad = mv

= 0.454 kg × 16 m/s

= 7.264 kgm/s

p of metal ball = mv

= 2 kg × -12 m/s

= -24 kgm/s

(Why is it a negative value? This is because the ball is moving towards the left, in the opposite direction of the other. So, we refer to speeds going to the left as negative here)

After the collision:

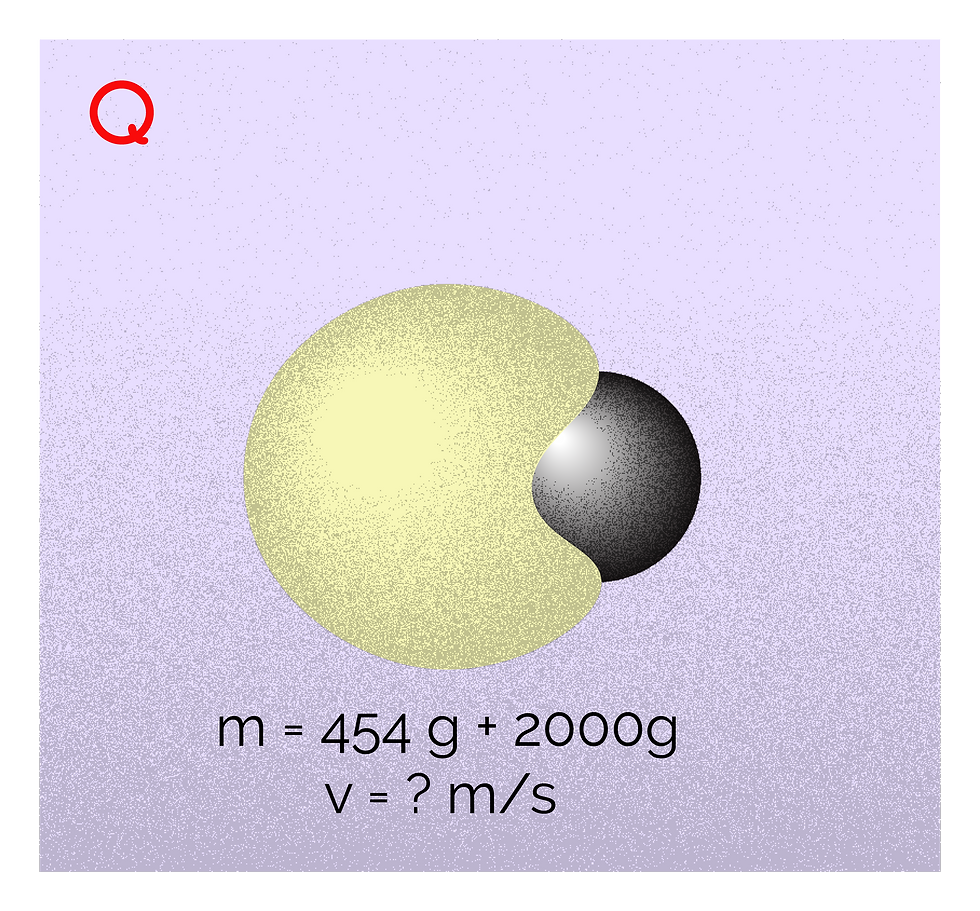
We can use the law of conservation of momentum here again:

p₁ + p₂ = p of combined object after collision

m₁u₁ + m₂u₂ = (m₁ + m₂) v

This equation looks different because the two objects become one object with one mass moving at a certain velocity.

7.264 kgm/s + -24 kgm/s = (0.454 kg + 2 kg) × v

-16.736 kgm/s = 2.454 kg × v

v= -16.736 kgm/s ÷ 2.454 kg

v = -6.82 m/s

The dough-metal abomination moves at 6.82 m/s (towards the left) which is back towards you. (It falls and cracks the tiles. I'm surprised you didn't realize that would happen)

It's important that you also realize how the law of conservation of linear momentum relates to Newton's Third Law, which states that every action has an equal and opposite reaction. So, in an isolated/closed system, if an object exerts force causing an increase in momentum in another, then that object loses momentum, meaning that the total momentum in the system remains constant.

Additional Reading

Hyperphysics lesson

OpenStax Link