Just a quick summary of the useful formulae and info from module 1. (In progress)
Remainder and Factor Theorem
Where a is the value of x when a divisor (x-a) is equated to zero and R is the remainder when f(x) is divided by x-a. f(x) is any polynomial.
Factors of a^n-b^n
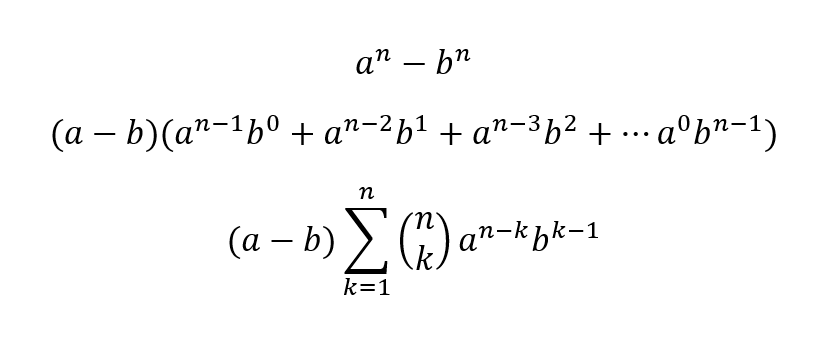
Cubic Roots
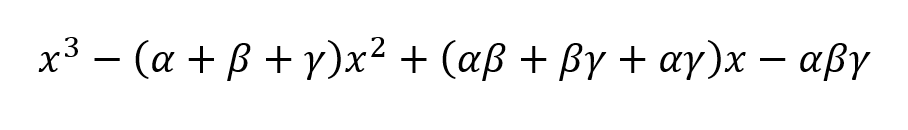
Where alpha, beta and gamma are the roots of the cubic equation.
Problems involving cubic roots related to equations usually take the form 'find the equation with roots...' So, here are two common forms to remember:
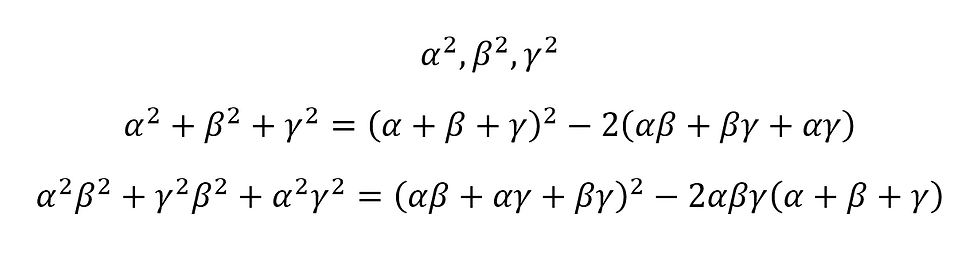
Summation notation for fancy boys and sigma males (sorry)
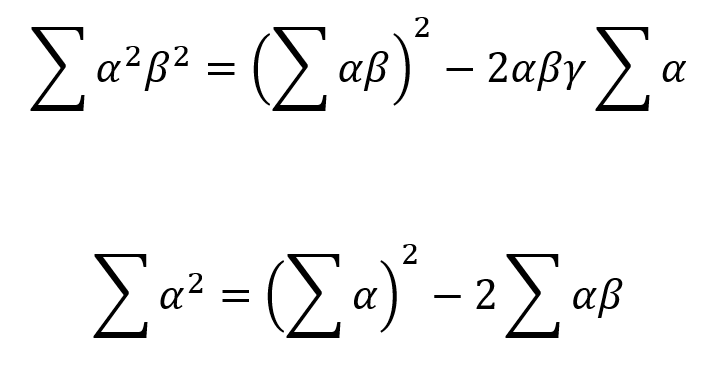
If the new roots are the squares of the previous roots, the sum and sum of the products of the roots could be found as shown above.
If the new roots are the inverses of the previous roots:
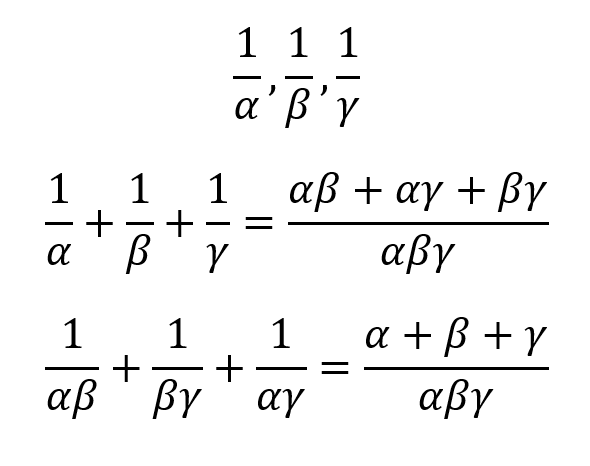
Sigma Notation/Summation
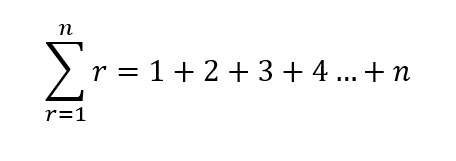
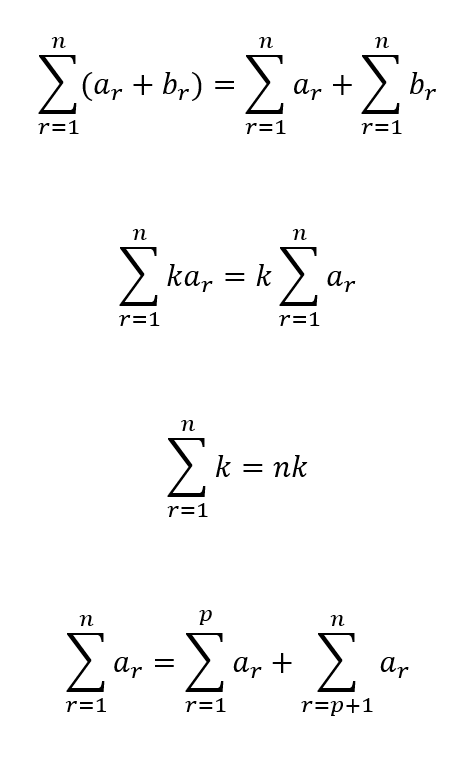
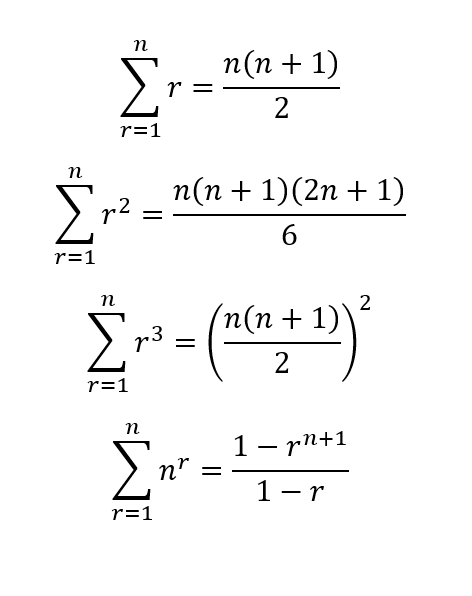
Modulus/Absolute Value Function
The definition of the modulus function:
The results of the modulus function:
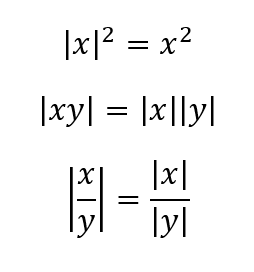
Inequalities involving the modulus function:
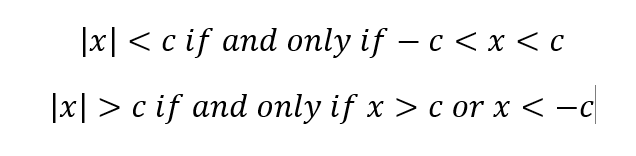
The triangle inequality proof:
Rational Functions
(Why are they here? Why not!)
A rational function is a function of the form:
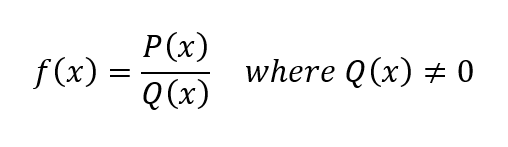
The domain of a rational function is all values of x for which the denominator (Q(x)) is not zero.
Asymptotes
Vertical- The vertical asymptote occurs where the denominator is zero, i.e. equate the denominator to zero and solve for x.
Horizontal- Depends upon the degree of the numerator (n) and denominator (m)
If n>m, there is no horizontal asymptote. However, if n=m+1, there is an oblique asymptote, where the asymptote's equation is the quotient of the denominator and numerator.
If n<m, then the x-axis is the horizontal asymptote.
If n=m, then the horizontal asymptote exists at
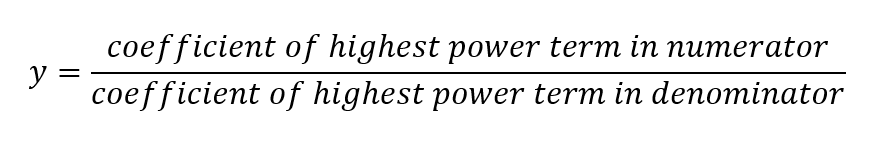
X-intercept- equate the numerator to zero and solve for x.
Tests, quizzes, and final exams are part of this traditional method. These tests usually test a person's ability to memorize information, understand ideas, solve problems, and think critically. Exams can be essay-based, multiple-choice, short response, or a combination of these. write my homework. Global Assignment Help are given to students to complete either individually or in groups. Essays, research papers, presentations, case studies, problem sets, and more can be included. Course concepts are assessed based on assignments through evaluation of student research, critical thinking, writing, creativity, and application.
Struggling with overwhelming assignments and tight deadlines? When you choose to pay for assignments, you’re investing in a streamlined path to academic success. Services like MyAssignmentHelp offer access to experienced professionals who understand the challenges of various subjects and can deliver well-researched, high-quality work. By opting to get expert assistance, you ensure your assignments are handled by specialists, boosting your chances of achieving top grades.
With experts available to craft assignments tailored to your requirements, you’ll save time and reduce stress, focusing on other important aspects of your education. Whether you’re dealing with a complex project or need help with basic tasks, turning to professional support guarantees better results. Make your academic journey smoother by entrusting your work to those who…
Good question. Well, I don't think it's such a problem, so I can suggest you use the site and how to play minesweeper. Overall, Minesweeper remains one of my favorite games because of its unique combination of strategy and luck. There is an element of surprise in every move I make that keeps me coming back for more.
The San Antonio Spurs contain introduced their formal 2022-2023 performing exercises camp roster.Below is the formal performing exercises camp roster for your San Antonio Spurs: Each and every franchise is authorized in the direction of convey 20 avid gamers all through the offseason, nevertheless they should reduce that range towards 15 regular contracts and a couple of 2-methods by way of the start out of the year.Alize Johnson and Tommy Kuhse are the greatest in all probability applicants toward buy the boot as they are upon Demonstrate 10 discounts, which utmost groups seek the services of towards fill out their camp ahead of rerouting mentioned avid gamers toward the G League.The Spurs return 11 avid gamers against a time in…